Should you care about “correlation”? Absolutely! Understanding correlation will help you master portfolio diversification.
Let’s begin with diversification. You’ve probably heard that diversification reduces investment risk, but how? Say there are only two companies: one that sells umbrellas and another that sells sunscreen. If a portfolio is completely invested in the company that sells umbrellas, it will have strong performance when it rains, but poor performance when the weather is sunny. The reverse occurs if the portfolio is only invested in the sunscreen company: sales will be high when the sun is out, but will be poor when clouds roll in. In this example, umbrellas and sunscreen are negatively correlated.So, what we have to do is attempt to find several assets that are responding to different forces in the economy.
To minimize the weather-dependent risk in the example portfolio, the investment should be split between the companies. As shown to below, with this diversified portfolio, returns are decent no matter the weather, rather than alternating between excellent and terrible.
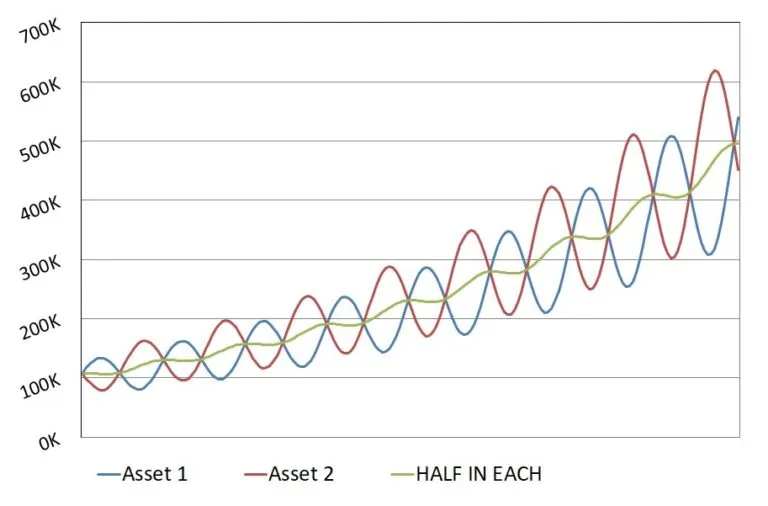
In reality, perfect negative correlation like the hypothetical umbrella/sunscreen portfolio is difficult to come by (if not impossible). So what we have to do is attempt to find several assets that are responding to different forces in the economy. Each such asset is, so to speak, marching to different drummer. If we have enough non-correlating assets in a portfolio, the odds of all of them falling into sync at any given point in time becomes very small. In fact, when one asset is taking a loss, there’s a good chance that one of the others will be making offsetting gains. Hence, with a well-diversified portfolio of non-correlating assets, the portfolio can be quite stable despite the fact that the underlying individual assets in the portfolio may be rising and falling dramatically in value (like in the graph above).
Correlation Risk Management
Now, just how do we identify a set of non-correlating assets that we can assemble into a low-risk portfolio? That is done using correlation “coefficients”. A correlation coefficient tells you what percentage of two assets’ price movements are driven by the same market forces. So, for example, if sunglasses and sunscreen are 100% correlated (having a coefficient of 1.00), their manufacturer’s stock prices would move in the same direction 100% of the time. On the other hand, the sunscreen and umbrellas from our previous example have a coefficient of -1.00 (negative 1.00), because their prices always move in opposite directions, which means they move together 0% of the time.
Now let’s take the center point — two assets whose correlation coefficient is 0.00. None of the forces driving their price movements are the same so their movements relative to one another will be arbitrary. That, however, means they are just as likely to move the same direction at any given time as they are to move in opposite directions. So, two assets with a correlation coefficient of 0.00 will move “together” 50% of the time (not 0%). So (somewhat counter intuitively) a 0.50 coefficient means they will probably move the same direction about 75% of the time (not 50% of the time).
the importance of correlation tables
With a general understanding of correlation coefficients, you can oversee your advisor’s investment recommendations. First, ask your financial advisor to provide you with correlation tables of the portfolio he is placing your account in. To help you understand the table, let’s go through two samples.
The first was provided by a student in our Management of the Investment Portfolio class that we teach through Cal State Fullerton and the second is a recent PIN portfolio. The table below forms a grid that correlates each asset with every other asset. (We chose to identify the funds by “Fund A,” “Fund B,” etc., in the Student Portfolio chart below and by “Fund 1,” “Fund 2” etc., in the PIN Portfolio chart on the next page rather than using their actual names to preclude the necessity of offering a prospectus for each fund.)
Find the top asset on the left column (Fund A). If you look at the first cell right of the fund name (i.e., the second column), you will see a correlation of 1.00.That’s because (if you look at the header for that second column) you are looking at the asset’s correlation with itself — not terribly useful. However, if you go to the third column (Fund B), you will see that this asset’s correlation with Fund A is 0.90. A check with the table above will tell you that such a high correlation is (in the author’s humble opinion) “worthless.” Continuing on to the right, its correlation with Fund C is 0.73, etc. Its correlations range between 0.73 at best to 0.93 at worst. This asset is adding very little diversification to the portfolio. Even if it has high returns, its high correlations mean it is increasing the probability of losses in difficult markets due to lack of diversification from the other assets in the portfolio – it is going to go down at the same time many of the other assets in the portfolio go down.
You can look at each asset in this same manner to determine, on an asset-by-asset basis, just how effective each is in diversifying the portfolio. You want assets with a preponderance of their correlations in the 0.70 and lower range. The bottom line of the table, in red font, is the average correlation of the assets with each other for the entire portfolio. Just use the overall average as an elimination criterion – a high average is unacceptable. A low average, however, does not mean every asset in the portfolio is good – each must be looked at individually, as explained above. With an overall correlation of 0.84 for the above portfolio, you can be pretty confident this portfolio is not going to provide a low-risk, well-diversified portfolio suitable for your needs. I’d tell the advisor to go back and come up with a better portfolio. Now let’s look at a recent PIN portfolio:
This portfolio shows an average correlation of 0.50 (“Very good” to “Excellent” according to Table 1). Does a 0.50 portfolio average correlation mean it is blemish free? No. As noted earlier, each asset must be evaluated individually. Do you see any assets in this PIN portfolio that are potentially less than ideal? I see one pair of assets (last column or bottom row) with a correlation of 0.82. According to the table on page 2, that is “poor to bad.” But, that is just the correlation against one of several funds. How do those two funds’ (Funds 3 and 7) correlation coefficients look versus the rest of the funds in the portfolio? They range from -0.09 (“outstanding”) to 0.48 (“excellent”). So that single “poor to bad” correlation of 0.82 can probably be ignored.Let’s pretend, however, that despite the 0.50 portfolio average correlation, we had found that one of the assets had correlations ranging from a low of 0.65 to 0.89 with three correlations above 0.80. That particular asset would probably not be improving the diversification of the portfolio and should be dropped or replaced.
Portfolio Diversification
Finally, remember that low or negative correlation must be associated with a decent return to provide a well-diversified portfolio with desirable returns. You can always go to the bank and get a 1% or 2% return with low risk. It is the combination of low correlation and decent or good returns that makes an ideal diversifier. That’s why loading up too much on bonds (which tend to have low returns) is not very productive. A modest allocation to bonds is generally beneficial; a heavy allocation tends to drag down the portfolio’s returns.
Minimizing the correlations among assets in the portfolio is the foundation of correlation risk reduction through effective diversification. The ability to glance through a correlation table and identify counter-productive assets will enable you to effectively supervise an advisor’s risk management and ability to properly diversify a portfolio. Applying the simple principles above and making correlation tables a condition of employment for your financial advisor is essential.
If you’re concerned about portfolio performance or whether you’re taking too much or too little risk, Prudent Investors offers portfolio evaluation services that help fiduciaries and individuals establish financial goals. Connect with our team to schedule a portfolio review today.


